Clase 17 Álgebra. Polinomios Raíces de un polinomio YouTube

Interpretación gráfica de las raíces de un polinomio. Interpretación gráfica de las raíces de un polinomio. Inicio. Noticias. Discutir las raíces de la ecuación x4-8x3+22x2-24x+m=0 según los valores del parámetro m ¿Qué interpretación puedes hacer de los valores obtenidos? Nuevos recursos. Earth, Sun and Moon;
Multiplicidad de las Raíces de un Polinomio YouTube

Primero graficaremos el polinomio para ver si podemos encontrar alguna raíz real de la gráfica: Podemos ver raíces en x = − 5, 3, lo que significa que (x + 5) y (x − 3) son ambos factores de este polinomio. Tendremos que dividir por ambos factores para descomponer el polinomio. Primero, dividimos por (x − 3): Y luego por (x + 5):
hallar raíces de polinomios YouTube

La forma estándar de una ecuación cuadrática es. 0 = ax 2 + bx + c. donde a, b, y c son todos los números reales y a ≠ 0. Si reemplazamos 0 con y , entonces obtenemos una función cuadrática. y = ax 2 + bx + c. cuya gráfica será una parábola . Los puntos donde la gráfica intersecta el eje de las x serán las soluciones a la ecuación.
Multiplicidad de Raíces de Polinomios con Ejemplos Neurochispas
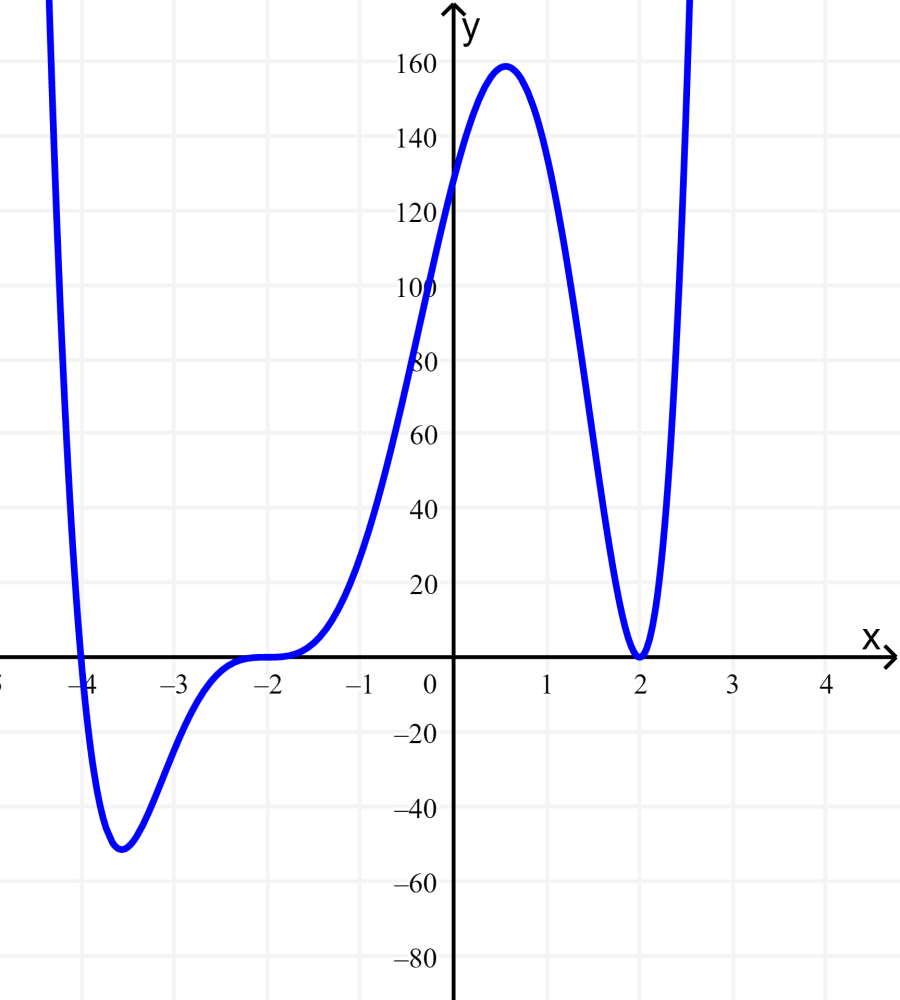
La conexión gráfica. La multiplicidad de un cero es importante porque nos indica cómo se comporta la gráfica del polinomio cerca del cero. Por ejemplo, observa que la gráfica de f ( x) = ( x − 1) ( x − 4) 2 se comporta de una manera diferente cerca del cero en 1 que del cero en 4 , que es un doble cero.
17 Raíces de un polinomio YouTube

Ya que un número es divisible por números positivos y negativos. De manera que las posibles raíces o ceros del polinomio son: ±1, ±2, ±3. Por lo tanto, debemos determinar el valor numérico del polinomio en todos esos valores. Y, para ello, sustituimos dichos valores en la expresión del polinomio donde haya una x:
Cómo calcular las raíces de un polinomio? Mica YouTube

Las funciones polinómicas también muestran gráficas que no tienen roturas. Las curvas sin roturas se denominan continuas. La figura 5.4.1 muestra una gráfica que representa una función polinómica y una gráfica que representa una función que no es polinomio. Figura 5.4.1: Gráfica de f(x) = x3 − 0.01x.
TEOREMA DE GAUSS. RAÍCES O CEROS RACIONALES DE UN POLINOMIO YouTube

Transcripción del video. usa los ceros reales de la función polinomio es igual a x al cubo más 3x al cuadrado más x 3 para determinar cuál de las siguientes podría ser su gráfica hay varios modos de atacar este problema 1 sería por ejemplo identificar visualmente cuáles son los ceros en estas gráficas y sustituirlos en la definición.
Raíces de un polinomio de grado 3 YouTube

Recordamos que para calcular el valor numérico de un polinomio hay que sustituir la variable del polinomio por un número. Cuando este valor sea cero, el número corresponderá con la raíz del polinomio. Vamos a verlo mejor con un ejemplo, que te ayudará a identificar los números que son raíces de un polinomio de los que no lo son. Tenemos.
Raíces polinomio de segundo grado. YouTube

En matemáticas, una raíz de un polinomio P(X) es un valor α tal que P(α) = 0. Por lo tanto, es una solución de la ecuación polinómica P(x) = 0 para la incógnita x, o también un cero de la función polinómica asociada.. Un polinomio distinto de cero con coeficientes en un determinado cuerpo puede tener raíces solo en un cuerpo «más grande», pero nunca tiene un número de raíces.
Polinomio con raíces reales YouTube

La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés. Raíces de polinomios. Este ejemplo muestra varios métodos diferentes para calcular las raíces de un polinomio. Raíces numéricas. Raíces mediante sustitución. Raíces en un intervalo específico
Método básico para comprobar raìces de un polinomio YouTube

Relación entre raíces y coeficientes de un polinomio. Sea α, β y θ son raíces de la ecuación x 3 + 4 x 2 − 2 x + 1 = 0 . ¿Cuál es el valor de la expresión α + β + θ ? Aprende gratuitamente sobre matemáticas, arte, programación, economía, física, química, biología, medicina, finanzas, historia y más.
Raíces de un polinomio usando división sintética YouTube

El orden del polinomio es k (es decir, el exponente de la mayor potencia de s que figure en el polinomio). k es igual al número total de raíces del polinomio; en el cómputo de este número cada raíz múltiple cuenta tantas veces como su propio orden. Las raíces de un polinomio pueden ser reales o complejas; si un número complejo es
maxresdefault.jpg

Ejemplo de polinomio de tercer grado con coeficientes enteros y tres raíces enteras (-1, 1 y 2) En matemáticas, un polinomio de grado con coeficientes reales o complejos siempre posee raíces complejas (sin olvidar que los números reales forman parte de los complejos), y teniendo en cuenta su posible multiplicidad.Forman un conjunto de puntos en el plano complejo.
* Hallar las raíces de un polinomio de grado 3 con calculadora científica Casio YouTube

Los ceros de una función f corresponden a las interseccciones de su gráfica con el eje x . Si f tiene un cero de grado impar, su gráfica cruza el eje x en ese valor de x . Si f tiene un cero de grado par, su gráfica toca el eje x en ese punto. Si esto te parece nuevo, recomendamos que leas nuestro artículo de ceros de polinomios.
PPT TEMA 6 DIVISIÓN DE POLINOMIOS PowerPoint Presentation ID4847813

Calculadora gratuita de raíces - Encontrar las raíces de cualquier función paso por paso. ¿Estás seguro de que quieres dejar este desafío? Al cerrar esta ventana perderás este desafío. con notación científica Números complejos Coordenadas Polares/Cartesianas Ecuaciones simultaneas Sistema de desigualdades Polinomios Números.
Polinomio a partir de sus raíces YouTube

Dado el gráfico de una función polinómica, escribir una fórmula para la función. Identifique las intersecciones en x del gráfico para hallar los factores del polinomio.; Examine el comportamiento del gráfico en las intersecciones en x para determinar la multiplicidad de cada factor.; Halle el polinomio de grado mínimo que contenga todos los factores determinados en el paso anterior.